https://www.acmicpc.net/problem/24416
24416번: 알고리즘 수업 - 피보나치 수 1
오늘도 서준이는 동적 프로그래밍 수업 조교를 하고 있다. 아빠가 수업한 내용을 학생들이 잘 이해했는지 문제를 통해서 확인해보자. 오늘은 n의 피보나치 수를 재귀호출과 동적 프로그래밍
www.acmicpc.net
def recur_fib(n):
global cnt1
cnt1 += 1
if n == 1 or n == 2:
cnt1 -= 1
return 1;
else:
return recur_fib(n-1) + recur_fib(n-2)
def dp_fib(n):
global cnt2
f[1], f[2] = 1, 1
for i in range(3, n+1):
cnt2+=1
f[i] = f[i-1] + f[i-2]
return f[n]
f = [0 for _ in range(41)]
n = int(input())
cnt1, cnt2 = 0, 0
recur_fib(n)
dp_fib(n)
print(cnt1 + 1, cnt2)사실 제가 생각했을 때 호출 횟수는 recur_fib(1), recur_fib(2)일 때도 계산해야 맞다고 생각하는데 문제에서는 아니라고 하니 빼주는 과정을 거쳤습니다. 또 재귀라서 미친듯이 호출하기 때문에 아마 python3로 제출하시면 시간초과가 날테니 pypy3으로 제출해주세요.
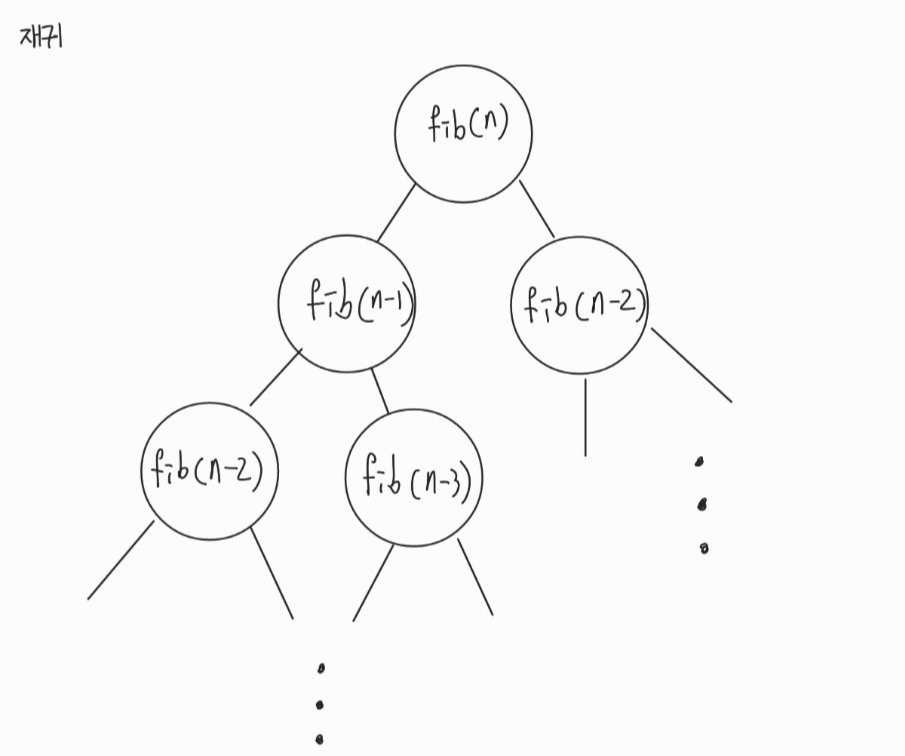
제가 짠 코드를 기준으로 설명을 드리면 recur_fib는 재귀 함수입니다. 재귀 함수는 함수 내에서 자기 자신을 호출하는 함수입니다. 따라서 n이 1이나 2일 때를 제외하면 1을 리턴하고 아닌 경우에는 recur_fib(n-1) + recur_fib(n-2)를 리턴하는 것을 볼 수 있습니다. 하지만 리턴을 저렇게 함수로 하면 당연히 해당 함수를 실행해야겠죠. 그래야 해당 함수를 실행했을 때 어떤 값이 나오는지를 알고 그걸 연산을 하든 반환을 하든 할테니까요. 즉 이런 피보나치 수열의 n번째 숫자를 구하는 경우에 있어서 재귀 함수는 계산을 위해서 이미 계산했던 것을 또 계산하는 과정을 계속해서 반복 실행하는 상당히 비효율적인 구조를 지니고 있다는 것을 알 수 있습니다. 아래 그림에서는 아주 적은 양만 썼지만 recur_fib(1)까지 가는 길에 있는 모든 계산을 모든 호출되는 함수에서 실행하는 겁니다. 그게 recur_fib(n)이든 recur_fib(n-1)이든 결국 recur_fib(1)까지 내려가서 계산하고 재귀 함수를 탈출하면서 처음 실행했던 n까지 올라오는 구조를 갖고 있어요.
그리고 dp_fib는 동적 계획법, 다이나믹 프로그래밍입니다. 다이나믹 프로그래밍이란 말만 들으면 도대체 이게 뭐지 싶어요. 프로그래밍 중에 막 뭐가 다이나믹하게 변화하나 싶기도 하구요. 해당 방법의 고안자는 처음엔 연구 예산을 따내기 위해서 이런 멋있는 이름을 지었다고 합니다. 어느 연구소나 이런 주제의 구색은 중요하긴 하죠. 약간 옆으로 샜는데 결국 다이나믹 프로그래밍의 핵심은 '미리 계산해뒀다가 필요할 때 불러 쓰기' 입니다. 이런 피보나치 수열의 문제가 단골 예시로 사용이 되는데요. 구조를 간단히 살펴보겠습니다.

먼저 1번과 2번에 각각 1을 집어넣습니다. 그리고 3번 부터는 그 앞의 두 수를 더하는 과정을 반복하죠. 이건 피보나치 수열을 구성하는 개념과 완전히 동일한데요. 위에서 봤던 재귀와 다른 점은 임의의 n번째 원소를 구하기 위해서 계속 연산식을 호출하는게 아니라 값만 불러와서 사용한다는 점입니다. 살짝 연산의 흐름도 좀 다른데요. 재귀의 경우 recur_fib(n)을 구하기 위해서 recur_fib(n-1)과 recur_fib(n-2)를 호출하고 recur_fib(n-1)은 recur_fib(n-2)와 recur_fib(n-3)을, recur_fib(n-2)는 recur_fib(n-3)과 ... 이런식으로 큰 숫자에서 작은 숫자로 내려가는 구조라면, DP는 f[3]을 구하고 f[4]를 구하고... 아래에서 위로 가는 흐름을 가지고 있습니다.
여기서 재귀처럼 위에서 아래로 가는 형식을 흔히들 탑다운(top-down), dp처럼 아래에서 위로 가는 경우를 바텀업(bottom-up) 구조라고 부릅니다. 어디선가 들어본 적 있으실 겁니다. 특히 이 쪽 분야에서는 너무 일상적으로 쓰는 말이기 때문에 알아두시면 다른 개념을 배울 때도 빨리 감 잡는데 도움이 되실거에요.
저는 해당 문제를 풀 때 이미 재귀나 dp 문제를 많이 풀어봤던 상태라서 좀 무심했었는데 많은 분들이 해당 포스팅을 찾아주시는 걸 보고 좀 이해가 되실 수 있도록 그림도 그려보고 좀 자세하게 작성하려고 노력해봤습니다. 이 글을 보시고 이해가 되시면 좋겠네요.
'Problem Solving > BOJ' 카테고리의 다른 글
| [BOJ][Python]1010번 풀이 (0) | 2022.05.27 |
|---|---|
| [BOJ][Python]17198번 풀이 (0) | 2022.05.25 |
| [BOJ][Python]1388번 풀이 (0) | 2022.05.24 |
| [BOJ][Python]15312번 풀이 (0) | 2022.05.24 |